1. Sierpinskitetraeder und Mengerschwamm zwei klassische platonische Fraktale
1.1. Zur Mathematikgeschichte
1.2. Existenz
der Grenzfigur
1.3. Fraktale
Dimension
1.4. Zu Querverbindungen
Sierpinskitetraeder, Mengerschwamm
1. Die beiden
bekannten platonischen Fraktale
Platonische Fraktale! worum geht es dabei?
Der Begriff ist nicht in der Literatur zu finden. Damit sollen ganz
wenige, spezielle fraktale geometrische Figuren aus platonischen Körpern
gemeint sein. Wir werden sehen, daß es mindestens fünf gibt,
und die werden heute vorgestellt. Aber es gibt mehr und ihre Tendenz ist
stark steigend, da viele Entdeckungen noch ausstehen.
Zwei werden die meisten von Ihnen kennen.
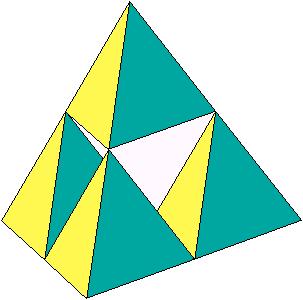
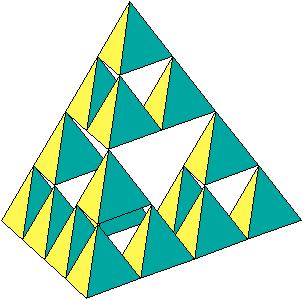
Im Bild:
 |
 |
 |
 |
|
Iterationsstufe 0 |
Iterationsstufe 1 |
Iterationsstufe 2 |
Iterationsstufe 3 |
 |
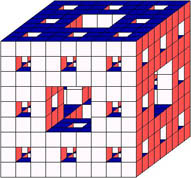
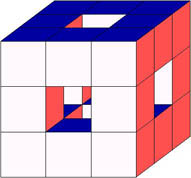 |
 |
 |
|
|
Iterationsstufe 0 |
Iterationsstufe 1 |
Iterationsstufe 2 |
Iterationsstufe 3 |
Platonische Fraktale Zu den neuen platonischen Fraktalen
1. 1. Zur Mathematikgeschichte
Geburtsjahr in der Literatur:
Das ebene Sierpinskidreieck entstand 1915 (Watzlaw
Sierpinski, siehe Lit.!) und vermutlich kurz darauf auch das nach Sierpinski
benannte Tetraeder, die Übertragung des ebenen Dreiecks in den Raum,
von dem mir keine Literatur von Sierpinski bekannt ist. Der Mengerschwamm
entstand 1926 (Karl Menger, siehe Lit.!),
als die formale Logik und Mengenlehre die Mathematik stark beeinflußten.
Zum ursprünglichen Anlass ihrer Konstruktion:
Beides sind Linienfiguren, bzw. -netze mit großer topologischer
Komplexität. Das Sierpinskidreieck ist ein Beispiel einer Linienfigur,
die nur aus Verzweigungspunkten besteht. Der Mengerschwamm ist ein Beispiel
einer topologisch universellen Kurve, einer Kurve, die alle anderen Kurven
inkl. Verzweigungen bis auf Verbiegungen (bzw. topologische Verformung)
homöomorph als Teilfigur enthält.
Topologische Dimension:
Beide Figuren haben die topologische Dimension 1. Sie sind Netze aus
Linien. Früher bezeichnete man solche komplexen Liniennetze auch als
Kurven und meinte damit Figuren mit der topologischen Dimension 1. Der
Begriff der topologischen Dimension wurde mathematisch streng erst
1921 und 1922 von Karl Menger (siehe Lit.!) und
dem Russen Urysohn (siehe Lit.!) fast gleichzeitig
neu definiert.
Exoten in der Mathematik
Beides sind also Objekte der mathematischen Grundlagenforschung. Besondere
exotische Punktmengen, um als Randfälle die Reichweite und Grenzen
von Begriffsdefinitionen in Topologie und Mengenlehre zu klären.
Bekanntheitsgrad:
Ihr Bekanntheitsgrad ist schwer abzuschätzen. Ich habe subjektiv
das Gefühl, daß sie ziemlich wenig beachtete geometrische
Figuren waren. Ich selbst bin in meinem Mathematikstudium weder dem Mengerschwamm
noch dem Sierpinskitetraeder begegnet.
Anders die Cantormenge, von der der Mengerschwamm eine dreidimensionale
Weiterführung ist. Sie kennt jeder Mathematiker. Man lernt sie als
Mathematikstudent in den Anfängervorlesungen als den schwer vorstellbaren
kuriosen Fall einer diskreten Menge kennen, die nur aus Häufungspunkten.
Auch die Kochkorve(= "Schneeflockenkurve") als eine nirgends differenzierbare
aber stetige Kurve kennt jeder Mathematiker. Solche Objekte wurden von
Weierstraß schon im letzten Jahrhundert diskutiert.
Fraktale Stiefkinder
Als Mandelbrot 1975 (Siehe Anmerkung 2!) den Fraktalbegriff
schuf und Mengerschwamm(die Bezeichnung stammt - soviel ich weiß
- von B. Mandelbrot) und Sierpinskitetraeder als zwei räumliche Figuren
mit in seine Fraktalsammlung aufnahm, wurden sie bekannter. Allerdings
waren es fast die einzigen räumlichen Fraktale. Diese wurden in der
Literatur im Vergleich zu den ebenen Fraktalen stiefmütterlich behandelt.
Vor allem wenn es um klassische Fraktale geht.
Das läßt sich in allen einschlägigen Büchern bis
in die heuteige Zeit verfolgen. Das geht parallel mit Verkümmern des
räumlichen Denkens im Mathematikunterricht der letzten Jahrzehnte.
In allerletzter Zeit scheint eine Trendwende zu entwickeln zu mehr räumlicher
Geometrie im Mathematikunterricht. Insofern liegen Experimente zu
räumlichen platonischen Fraktalen gut im Trend.
Die ersten Bilder?
Geht man spaßeshalber der mathematikgeschichtlichen Frage nach,
wann und wo die ersten Abbildungen der beiden Figuren veröffentlicht
wurden, so staunt man, wie wenig Bilder es überhaupt gab.
Sierpinski hat in seinen Veröffentlichungen im Vergleich zu Menger
häufiger Abbildungen zu solchen Figuren gezeichnet. Zu dem nach ihm
benannten und sehr bekannten Sierpinskidreieck hat er sehr detaillierte
Bilder gezeichnet. (Bilder zum Sierpinskitetraeder fehlen aber?? siehe
Anmerkung 1!)
Menger hat in den ersten Veröffentlichungen von seiner "Universellen Kurve" nicht ein einziges Bild gezeichnet. Für einen der Hauptorganisatoren des berühmten Wienerkreises, wo die führenden Logiker und Philosophen der Zeit verkehrten (Popper Russel, Gödel, Wittgenstein, Sierpinski, Brower, ...) galten solche Zeichnungen vielleicht als nicht oportun. Erst ziemlich spät findet man in einer Veröffentlichung von ihm er ein Bild dieser Menge. Die früheste Abbildung, welche ich gefunden habe steht in dem 1969 erschienen Buch Blumenthal/ Menger / ... Studies in Geometry
Der Geburtshelfer
Zu dieser Zeit gab es schon bessere Computer. Es sei festgehalten,
daß Mandelbrots Fraktalbegriff ein Computerkind ist. Die grafischen
Fähigkeiten der Rechner waren ein unentbehrlicher Geburtshelfer.
Platonische Fraktale Zu den neuen platonischen Fraktalen
1. 2. Existenz einer
Grenzfigur
Auf den Abbildungen (Siehe oben!)
sieht man bekanntlich noch keine der platonischen Fraktale sondern nur
die ersten Iterationsstufen. Die eigentlichen Figuren sind die Grenzfiguren,
Gedankengebilde, die niemand zeichnen kann, die letztlich sich auch niemand
genau vorstellen kann.
Ausprägungen des Unendlichen in der Mathematik. Leger ausgedrückt,
muß man "unendliche lange iterieren". Auch Menger und Sierpinski
formulierten vor 80 Jahren wenig streng: "Führt man diesen Konstruktionsschritt
unendlich oft aus, so erhält man die universelle Kurve.... ".
Macht es Sinn, so etwas zu sagen? Existiert die Grenzfigur? Mit der
Mengenlehre und dem Begriff des Aktual-Unendlichen kein Problem.
Als Punktmenge im IR^3 sind diese Mengen eindeutig bestimmt.
In der Schule kann man über die Existenzfrage zu diesen Fraktalen geometrischen Gebilden schöne Diskussionen zum Unendlichen in der Mathematik provozieren. Paradoxien bei Geometrische Figuren motivieren die Schüler dabei stärker als die bei Zahlen!
Der Grenzwertbegriff von Mengenfolgen bzw. eine Metrik in der Potenzmenge eines metrischen Raumes, von Hausdorff konstruiert, ist für die Schule zu abstrakt.
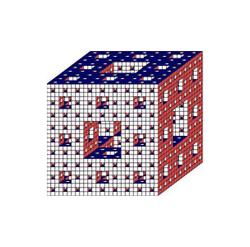
Beim Mengerschwamm [=: M] kann man die Punkte im dreiadischen Ziffernsystem wie den Cantorstaub [=: C] sehr einfach hinschreiben.
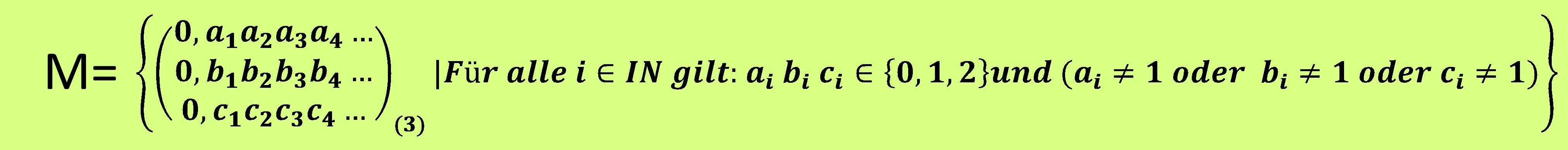
In fächerübergreifenden außermathematischen Diskussionen
ist die Existenz ein ganz anderes Problem.
Unter den Nichtmathematikern gibt es anerkannte Wissenschaftler, die
über die Existenz dieser abstrusen Grenzfiguren allenfalls nur lachen,
aber Mandelbrot und seinen Fraktalbegriff als Bereicherung auch ihrer Wissenschaft
voll aktzeptieren.
Interessant ist der alternative Standpunkt, daß lediglich die
Existenz eines nicht endenden Prozesses (als konstruktivistische mathematische
Begriffsbildung nicht uninteressant!) akzeptiert wird, aber nicht die Existenz
einer Punktmenge als Endprodukt.
Platonische Fraktale Zu den neuen platonischen Fraktalen
Fraktale sind nicht zuletzt deswegen besonders beeindruckend für die Schüler, weil die gewohnte Vorstellung der 1-, 2- und 3-Dimensionalität der geometrischen Figuren aufgegeben wird. Genauso wie den Sprung in die Vierte Dimension oder höhere Dimension vergißt ein Schüler vermutlich nie den Schritt zur gebrochenen Dimension etwa zu log(4)/log(3) als der Dimension der Schneeflockenkurve zwischen den natürlichen Zahlen 1 und 2.
Es gibt bekanntlich eine Reihe von verschiedenen Definitionen zur fraktalen Dimension, die leider auch nicht mathematisch äquivalent sind. Weiterhin gibt es ein weites Feld von verschiedenen Interpretationen und inhaltlichen Deutungen der fraktalen Dimension von "Maß für geometrische Komplexität", Maß für Dichte der Punkte", "topologisch nicht Linie und nicht Fläche", ... . Die mathematisch zufriedenstellendste nach Felix Hausdorff benannte strenge Definition (siehe Literatur Hausdorff 1919) ist für die praktische Anwendung am wenigsten handlich und auch für den Mathematikunterricht praktisch ungeeignet. In der Schule begnügt man sich mit wenigen Spezialfällen, der sogenannten Selbstähnlichkeitsdimension sowie Boxcounting- und Zirkelzähldimension.
Ich möchte an dieser Stelle einmal die für den MU gut geeignete und übliche Einführung der Selbstähnlichkeitsdimension kurz zusammenfassen, und dabei eine möglichste nüchterne Interpretation, als "Wachstumsexponent beim Zoomen" bezeichnet, unterstützen. An weiteren zusätzlichen Interpretationen der fraktalen Dimension einer Punktmenge möchte ich mich nicht beteiligen.
Der Gedankengang (Siehe auch Abbildung):
1. Man baut auf der Erfahrung, bzw. auf der im Mathematikunterricht
mit Längen-, Flächen- und Raummaßen in Verbindung mit der
zentrischen Streckung (Siehe Anmerkung 3!) gelernten
Erkenntnis auf :
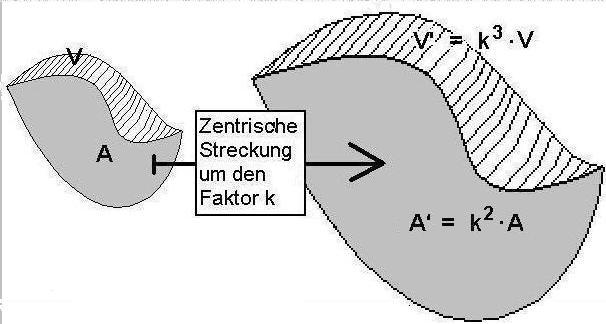
Wird eine Kartoffelfigur mit der Schnittfläche A um den Faktor k gestreckt, so wächst A mit k^2 und V mit k^3. |
Bei n-dimensionalen Maßen gibt es die entsprechende Fortsetzung
mit der n-ten Potenz des Streckfaktors.
Auch darauf, daß der "triviale" Randfall n = 1, also das Strecken
von Linien mit der neuen Länge L' = k^1* L = k^Dim * L, gut in dieses
Schema paßt, wird der Schüler aufmerksam gemacht.
2. Man entdeckt, daß dabei (nicht nur zufällig!)
die Dimension 2, 3, 4, 1, n als Exponent im Wachtumsfaktor des jeweiligen
Maßes vorkommt.
 |
3. Bei den Fraktalen macht der Schüler nun die überraschende
Erfahrung, daß die Schneeflockenkurve oder das Sierpinskidreieck
und andere Punktmengen oder "Punktsubstrate" Schäume, Liniengewickel
oder wie auch immer bezeichnet weder quadratisch noch kubisch wachsen.
Zum Beispiel wächst ein Sierpinskidreeick beim Zoomfaktor 2 um das
dreifache.
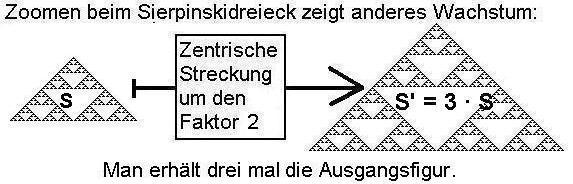 |
Überraschend ist für den Schüler auch, daß bei
diesen Figuren das bekannte Messendurch Einschachteln von innen und außen
mit immer kleineren Quadraten (Flächen) oder Würfeln(Volumen)
nicht mehr greift, da es nur die Werte Null oder Unendlich liefert.
Suggestiv ausgedrückt kommt man zu Figuren mit keiner Fläche
aber unendlicher Länge(Sierpinskidreieck) oder unendlicher Fläche
ohne Volumen (Mengerschwamm).
4. Warum soll man sich nicht bei der neuen Wachstumsgleichung auch den Wachstumsexponenten ermitteln. Bei den gewohnten euklidischen Figuren war er die Dimension. Es bietet sich an, auch jetzt bei Fraktalen von einer Dimension zu sprechen.
 |
Der Wachstumsexponent Dim in 3*S = 2^Dim*S ( <==> Dim = log(3)/log(2) ) wird als Dimension bezeichnet, und ist dann eine Zwischendimension zwischen den Dimensionen 1 und 2.
Es sei darauf hingewiesen, daß man auch bei den Fraktalen passend zu ihrer Dimension ähnlich wie bei Längenmaß von Linien und Flächeninhalt bei Flächen elementar ein Maßsystem aufbauen kann. Elementar in dem Sinn, daß man wie Größenbereichen üblich zählt, wie oft eine Maßfigur in eine zu messende Figur hineinpaßt. Unter Einbeziehung von Grenzwertbildungen läßt sich das Maß auf einen großen Bereich ähnlich gebauter Punktmengen anwenden. (Siehe "Das Schneeflockenmeter... ")
Die (Be-)Deutung der gebrochenen Dimension als Wachstumsexponenten
beim Zoomen trifft eine wesentliche Eigenschaft der Hausdorffdimension.
Diese Idee läßt sich in der Schule gut vermitteln, ohne
dass man die schwierige, allgemeine, auf jede Menge anwendbare Hausdorff-Dimension
verstehen muß.
Das Sierpinskitetraeder, ein Fraktal mit nichtgebrochener fraktaler
Dimension
Beim Sierpinskitetraedergestrick ergibt sich die verblüffende
Besonderheit einer glatte Zahl als Wachstumsexponent sprich fraktaler Dimension
Dim = log(4)/log(2) = 2.
Man kommt kaum in die Versuchung, dieses seltsame Gebilde als flächig
also als "natürlich zweidimensional" aufzufassen.
Trotzdem: Mandelbrot hat in seinem berühmten Buch Die
fraktale Geometrie der Natur S. 154. erläutert,
wie eine parallele Projektion dieses total durchsichtigen Gebildes entlang
einer Seitenmittenachse dann auf der Projektionsfläche ein Quadrat
absolut dicht ausfüllt.
Von einer idealen parallelen Lichtquelle würde also das Sierpinskitetraeder
in dieser Richtung nicht einen Lichtstrahl durchlassen. Dreht man es allerdings
ein winziges Stück zur Seite und nach oben, dann läßt es
praktisch alles Licht durch. Vielleicht wird diese Figur mal als Lichtfilter
einen Nutzen haben, wo bestimmte Richtungen ausgeblendet werden müssen.
Platonische Fraktale Zu den neuen platonischen Fraktalen
Querverbindung: vom Sierpinski-Dreieck zur Sierpinski-Pyramide:
Als interessantes Beispiel einer innermathematischen Querverbindung
der Fraktale sei die Möglichkeit genannt, daß man die vielen
Experimente zum Sierpinskidreieck, wie sie etwa in dem Band Bausteine
von Peitgen Saupe Jürgens beschrieben werden von der Ebene in den
Raum auf die Sierpinskipyramide übertragen kann. Hier finden
sicherlich Möglichkeiten für mathematische Facharbeiten.
|
|
|
| Binomische Formeln (a + b)^n
mit den Binomialkoeffizienten |
Trinomische Formeln (a + b + c)^n
mit den Trinomialkoeffizienten |
| Pascalsches Dreieck
Kreis- (Bierdeckel-) pflasterung Die ungeradzahligen Zahlen bilden das Sierpinki-Dreieck |
Pascalsche Pyramide
(Keplersche) Kugelpackung Die ungeradzahligen Zahlen bilden die Sierpinki-Pyramide |
| Ebener zellulärer Automat | Räumlicher zellulärer Automat |
| ebenes Chaosspiel | räumliches Chaosspiel |
Das Ergebnis des zellulären Automaten, die Sierpinski-Pyramide
aus den ungeraden Zahlen der Trinomialkoeffizienten hat Evgeny Devidov
(auf Anfrage des Verfassers hin) in wenigen Tagen als wunderschenes frei
drehbares Modell aus Kugeln in Java programmiert.
Es ist im Internet zu besichtigen: Evgeny
Demidov.
Die Cantorsche Verwandtschaft
Der Mengerschwamm ist ein direkter Abkömmling der Cantormenge.
!!Hinweis!!
An dieser Stelle wurden die Mengendarstellungen als Vereinung aus karthesischen Produkten gelöscht.
Sie waren leider fehlerhaft.
Wilhelm Sternemann, 30.März 2015
Die Systematik Cantorsche Verwandtschaft sei im Überblick dargestellt.
|
Cantormenge
|

C x C |

C x C x C |
?
C x C x C x C |
|
Einheitsintervall
I |

Sierpinskiteppich |
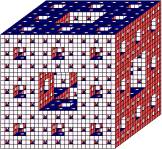 > >
Mengerschwamm |
?
|
|
Einheitsquadrat
I x I |
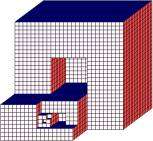
"Mengerschaum" |
|
|
|
Einheitswürfel
I x I x I |
?
|
Die Inspirationsquelle Mengerschwamm
Der Mengerschwamm scheint die Anwender in der Grundlagensforschung
von Industrie und Wissenschaft stark zu inspirieren. Daß er eine
unendlich große Fläche und kein Volumen hat, hat einige Forscher
in der Physik und Technik in Uni und Wirschaft zu weiteren Überlegungen
angeregt.
Das beweisen mehrere interessante Kontakte, die sich nach dem Artikel
in Spektrum der Wissenschaft entwickelten, über die sich Lehrer und
Schüler gleichermaßen freuen.
Zu den neuen platonischen Fraktalen
Zurück zur Titelseite
Platonische Fraktale Zu den neuen platonischen Fraktalen
Es handelt sich hier um Auszüge aus einem
Vortrag am 7. 11. 2000
am Heinrich Behnke Seminar, Friedrich Wilhelms Universität Münster
im Kolloquium über Geschichte und Didaktik der Mathematik
(Offizielles Thema:) Platonische Fraktale - zu ihrer Mathematik
und wie Schüler der Klasse 10 sie zum Anfassen herstellen
von Wilhelm Sternemann
Anmerkung 1: Das Sierpinski-Tetraeder habe ich in
den Publikationen von Sierpinski nicht gefunden. Es ist mir nicht bekannt,
ob das Sierpinskitetraeder von Sierpinski stammt, oder ob es einfach nach
ihm benannt wurde. Ich wäre sehr dankbar, wenn mir jemand dazu eine
Literaturstelle nennen könnte.
Zumindest das stammt das ebene Sierpinski-Dreieck,
von dem das Tetraeder eine räumliche Entsprechung ist, von Sierpinski.
In Mandelbrots "Fraktale Geometrie der Natur" wird
das Tetraeder ohne den Namen Sierpinski als ein "fraktales schiefes Gewebe"
aufgeführt mit einer von V. Alan Norton berechneten Abbildung. Diese
Abbildung ist die früheste, die mir bekannt ist.
Mandelbrot macht dort die fraktale Dimension 2 plausibel, indem
er beschreibt, wie man die Figur auf ein ausgefülltes Quadrat projizieren
kann.
Anmerkung 2: Mandelbrot selbst bezeichnet in "Die fraktale Geometrie der Natur" (S.14) 1975 als das Entstehungsjahr. "... Obwohl die fraktale Geometrie als solche aus dem Jahre 1975 stammt, ....". Eine entscheidende Rolle spielt wohl dabei seine Arbeit Les objets fractals: forme, hasard et dimension.
Anmerkung 3: Andere Umschreibungen wie. "Zoomen"
oder "Wechsel der Skalierungsmaßstabes" zeigen seine aktuelle Bedeutung.
Literatur
Sierpinski, Waclaw. Sur une courbe dont
tout point est un point de ramification. Comptes Rendus hebdomadaires
des séances de l'Acadeémie des Sciences 160, p. 302-305 Paris
1915
Menger, Karl "Über die Dimensionalität
von Punktmengen (Erster Teil)" im Jahr 1923 Monatshefte für Mathematik
und Physik (Heft 33), S. 148-160,
und "Über die Dimensionalität von Punktmengen (Zweiter
Teil)", im Jahr 1926, Monatshefte für Mathematik und Physik (Heft
34), S: 137-161(?)
Menger, Karl. "Allgemeine Räume und
Cartesische Räume". Zweite Mitteilung: "Über umfassendste n.dimensionale
Mengen". Proceedings Academie Amsterdam 29, S. 1124ff, 1923
Blumenthal, Leonhard M./ Menger Karl. Studies
in Geometry. W. H. Freeman and Company Sanfrancisco 1970
Mandelbrot, Benoît B. Fraktale Geometrie
der Natur 1987 (engl. Orig. 1977)
Mandelbrot, Benoît B.Les objets fractals:
forme, hasard et dimension In: Flammarion. Paris 1975
Urysohn, M. P. "Les multiplicites cantoriennes"
Comptes Rendus hebdomadaires des séances de l'Acadeémie des
Sciences 175 II p. 440-442 Paris 1922
M. Komorek/ R. Duit/ M. Schnegelberger
(Hrsg.). Fraktale im Unterricht.
IPN-Materialien. Kiel 1998
W. Sternemann. Das "Schneeflockenmeter". Ein
Denkanstoß zum Messen von Schneeflockenkurven. In M. Komorek/
R. Duit/ M. Schnegelberger (Hrsg.), Fraktale im Unterricht IPN-Materialien
Kiel 1998
Hausdorff, Felix Dimension und äußeres
Maß Mathematische Annalen 79 S.157-179, 1919
*) Für die Hilfe bei der Zusammenstellung
danke ich Herrn Prof. Dr. Hans Joachim Samaga
Universität Hamburg - FB Mathematik
Platonische Fraktale Zu den neuen platonischen Fraktalen