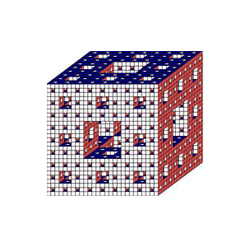1.1. Zur Mathematikgeschichte

   1.2. Existenz der Grenzfigur

   1.3. Fraktale Dimension

   1.4. Zu Querverbindungen
 
 
 

2. Experimente mit "Platonischen Fraktalen" in der Schule
 
 
 

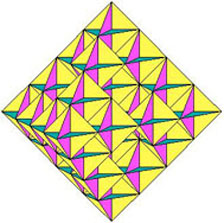
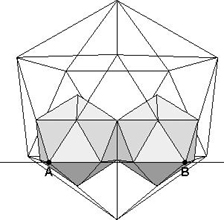
   2.1. Die Konstruktionsvorschrift (Entstehung und Präzisierung)

   2.2. Anwendung auf ebene reguläre Polyeder

   2.3. Anwendung auf das Oktaeder

   2.4. Anwendung auf das Ikosaeder

   2.5. Anwendung auf das Dodekaeder

   2.6. Angaben zur konkreten Herstellung unserer Modelle

   2.7. Ausblicke auf weitere Möglichkeiten zu mathematischen Experimenten
 

Anmerkung:
Es handelt sich hier um Auszüge aus einem Vortrag am 7. 11. 2000
am Heinrich Behnke Seminar, Friedrich Wilhelms Universität Münster
im Kolloquium über Geschichte und Didaktik der Mathematik
(Offizielles Thema:) Platonische Fraktale - zu ihrer Mathematik und wie Schüler der Klasse 10 sie zum Anfassen herstellen
von Wilhelm Sternemann

Diese Seite wird ständig aktualisiert und ist deshalb ein laufendes Projekt. Daher bitte ich um Verständnis für kleinere Fehler.

Über Kritik und Anregungen würde ich mich freuen.
sternemann@t-online.de
 

Literatur
Sierpinski, Waclaw. "Sur une courbe dont tout point est un point de ramification." Comptes Rendus hebdomadaires des séances de l'Acadeémie des Sciences 160, p. 302-305 Paris 1915
Menger, Karl "Über die Dimensionalität von Punktmengen (Erster Teil)" im Jahr 1923 Monatshefte für Mathematik und Physik  (Heft 33), S. 148-160,
und "Über die Dimensionalität von Punktmengen (Zweiter Teil)", im Jahr 1926, Monatshefte für Mathematik und Physik (Heft 34), S: 137-161(?)  
Menger, Karl. "Allgemeine Räume und Cartesische Räume". Zweite Mitteilung: "Über umfassendste n dimensionale Mengen". Proceedings Academie Amsterdam 29, S. 1124ff,  1923
Blumenthal, Leonhard M./ Menger Karl. "Studies in Geometry." W. H. Freeman and Company Sanfrancisco 1970
Mandelbrot, Benoît B. "Fraktale Geometrie der Natur" 1987 (engl. Orig. 1977)
Mandelbrot, Benoît B."Les objets fractals: forme, hasard et dimension" In: Flammarion. Paris 1975
Urysohn, M. P. "Les multiplicites cantoriennes"  Comptes Rendus hebdomadaires des séances de l'Acadeémie des Sciences 175 II p. 440-442 Paris 1922
M. Komorek/ R. Duit/ M. Schnegelberger (Hrsg.). "Fraktale im Unterricht." IPN-Materialien. Kiel 1998
W. Sternemann. "Das 'Schneeflockenmeter'. Ein Denkanstoß zum Messen von Schneeflockenkurven." In M. Komorek/ R. Duit/ M. Schnegelberger (Hrsg.), "Fraktale im Unterricht  "IPN-Materialien Kiel 1998 (Internetversion)
Hausdorff, Felix  "Dimension und äußeres Maß"; Mathematische Annalen 79 S.157-179, 1919

*) Für die Hilfe bei der Zusammenstellung danke ich  Herrn Prof. Dr. Hans Joachim Samaga      Universität Hamburg - FB Mathematik
  Eine aktuellere Darstellung zum Thema im Spektrum Online, März 2010.



-----