Gescheiterte und gelungene Zähmungen eines "maßlosen" Monsters Siehe Anm. 0) und 1) Inhalt 1 Die seltsame Kurve - das "Monster": 2 Die Frage nach einem Maß: 2a Scheitern Nr. 1 - Eine Kurve, die für eine Längenmessung zu lang ist. 2b Scheitern Nr. 2 - Ein Gekräusel, das für Flächenmessung nicht dicht genug ist 3 Das Messen ist zweimal gescheitert! 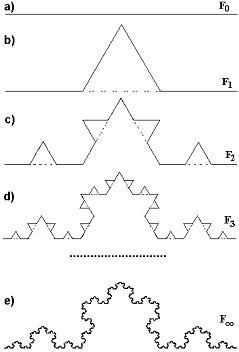Nun eine Lösung, ein passender Messversuch 4 Protokolle als Messgehilfen 5 Selbstähnlichkeitsdimension und Schneeflockeninhalt 6 Schluß Literatur 1 Die seltsame Kurve - das "Monster": Abb. 1 Erzeugung der Schneeflockenkurve Diese im Bild konstruierte Kurve hat unter den mathematischen Figuren einen hohen Bekanntheitsgrad. Zumindest kennt sie jeder Mathematikstudent aus den ersten Semestern als ein Beispiel einer Kurve, die nirgends glatt ist sondern nur aus Spitzen besteht. Zu ihrer Konstruktion geht man von einer Einheitsstrecke aus, sie sei als Figur F(0) bezeichnet. Der Konstruktionsprozeß besteht in einer Iteration. Man erzeugt in Gedanken aus der erreichten Figur immer wieder eine neue und zwar immer nach der selben Vorschrift: In jeder Strecke wird das mittlere Drittel, wie in Abb. 1b dargestellt, durch zwei Seiten eines gleichschenkligen Dreiecks ersetzt. Die nach dem n-ten Iterationschritt erhaltene Figur werde als Figur F(n) bezeichnet. Zur Verdeutlichung sind in den Abbildungen 1a) bis d) die Konstruktionsschritte F(0), F(1), F(2) und F(3) dargestellt. Unter der Schneeflockenkurve versteht man nun die in Abb. 1e angedeutete Grenzfigur F(unendl), die man „nach unendlich vielen Konstruktionsschritten" erhält. Anm. 2) Die Schneeflockenkurve wurde von Helge von Koch um 1904 erstmalig beschrieben, und zwar als Beitrag zur mathematischen Grundlagenforschung (Siehe Literatur H. Koch 1904!) und heißt deswegen in der Mathematik auch „Kochkurve“. Es ging damals um die Abgrenzung der Begriffe Stetigkeit und Differenzierbarkeit. Die Kochkurve ist überall stetig (= "durchgehende Funktionskurve ohne Lücken und Sprünge") und nirgends differenzierbar (= nirgends glatt) sondern nur aus Spitzen bestehend. Bekannt ist auch die Selbstähnlichkeit der Schneeflockenkurve, ein interessante Symmetrieeigenschaft, die in diesem Beitrag mehrmals von benutzt wird. Teile der Figur sind exakte verkleinerte Kopien der ganzen Figur. Eine solche Eigenschaft gilt als typisch für sog. Fraktale, eine in den siebziger Jahren von B. Mandelbrot ins Leben gerufenen Bezeichnung für einer Reihe von komplexen geometrischen Figuren. Gibt es die Figur überhaupt? Diese Grenzfigur kann niemand zeichnen. Niemand hat sie je gesehen! Gibt es sie überhaupt? Oder ist sie ein Hirngespinst? Diese spannende Diskussion ist an dieser Stelle nicht das Thema. Nur eine grobe kurze Antwort sei versucht: Wenn man die Existenz der reellen Zahlen als Punkte auf der Zahlengeraden akzeptiert inclusive der irrationalen Punkte (wie z.B. Wurzel(2), der Länge der Diagonalen des Quadrates mit der Kantenlänge 1), dann liegt von jedem Punkt der zweidimensionalen Koordinatenebene eindeutig fest, ob er zur Grenzkurve F(unendl) gehört oder nicht. Also muss man auch die Existenz dieser Grenzkurve F(unendl) akzeptieren. Die Frage stellt sich, ob wir denn überhaupt wissen, wie diese Figur aussieht, wenn sie noch niemand gesehen hat. In Abb. 2e etwa wurde eigentlich gelogen. Wir haben den Computer die Annäherungsfigur F(6) zeichnen lassen und daran den Namen F(unendl) gesetzt. Trotzdem sind die realen Annäherungsfiguren der Iteration unser Trostpflaster. Es stimmt zwar nicht eine der Linienstücke mit der Kochkurve überein, da jede Linie im nächsten Iterationsschritt wieder aufgebrochen wird. Die Grenzfigur hat keine Linienstücke mehr. Aber jeder einmal benutzte Eckpunkt gehört zur Grenzfigur. Man kann die Abweichungen dieser falschen Figuren von der Grenzfigur beliebig klein machen. Also „stimmt“ die Vorstellung von der Grenzfigur, die aus diesen Annäherungen gewonnen wird. Als anderes Beispiel einer solchen Grenzfigur ist den Schülerinnen und Schülern häufig aus der Mittelstufe der Kreis bekannt, wenn er durch n-Ecke angenähert wird. Dabei wird u.a. die Länge der Kreislinie und der Inhalt der Fläche bestimmt und dazu die Zahl p eingeführt. Das mathematische „Monstrum“ Schneeflockenkurve erweist sich im Vergleich zur Kreislinie als schwieriger und seltsamer. Zum Anfang 2 Die Frage nach einem Maß: Wie schon anfangs erwähnt, gilt in diesem Beitrag die Leitfrage nicht den qualitativen Merk-malen sondern dem Messen. Die Schneeflockenkurve ist eine unendlich filigran gekräuselte Linie. Man sieht in Abb. 2, daß von diesem feinen "Gekräusel", von dem „Substrat“ Schnee-flockenkurve zwischen den Punkten A und B offensichtlich mehr vorhanden ist als zwischen B und C. Vielleicht sechseinhalb mal soviel? Oder ist es mehr oder ist es weniger? Das soll im folgenden gemessen werden. Aber wie? Was ist das richtige Maß? 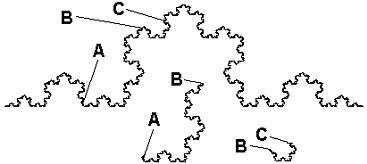Abb. 2: Schneeflockenkurve mit Teilausschnitten Zum Anfang 2a Scheitern Nr. 1 - Eine Kurve, die für eine Längenmessung zu lang ist Allen Schülerinnen und Schülern, denen die Schneeflockenkurve jemals begegnet ist, ist bekannt, daß eine klassische Längenmessung nicht möglich ist. Denn die Länge der Ausgangsfigur wird mit jedem Iterationsschritt um den Faktor 4/3 vergrößert. Damit wächst die Länge der Annäherungsfiguren exponentiell über jede Grenze. Andererseits muss jede Annäherungsfigur als Streckenzug kürzer sein Grenzfigur, da sie in jedem Fall noch zusätzliche Windungen enthalten muss. Bei Weiterführung des Grundsatzes von Euklid, daß eine Strecke die kürzeste Verbindung zweier Punkte ist, bleibt „unendlich“ die einzige Möglichkeit für die Länge der Schneeflockenkurve. Noch paradoxer wird der Sachverhalt dadurch, daß auch alle Teilstücke einer Schneeflocken-kurve unendliche Länge haben. Es stellt sich die Frage, wieviele unendlich lange Teilstücke man in einer Schneeflockenkurve aneinandergereiht vorfinden kann. Es sind mehr als jede endliche Zahl, sind es abzählbar viele oder überabzählbar viele? Und jedes hat wiederum ge-nausoviel unendlich lange Teilstücke usw.! Es wird deutlich, wie beängstigend lang dieses „Längenmonster“ Schneeflockenkurve ist, obwohl es diese Länge auf einem begrenzten Flächenstück entfalten muß. Zum Anfang 2b Scheitern Nr. 2 - Ein Gekräusel, das für Flächenmessung nicht dicht genug ist Auf die Idee, dieser gekräuselten Linie einen Flächeninhalt zuzuordnen, kommen Schülerin-nen und Schüler nicht so schnell. Die bekannte „Drachenkurve“ oder auch die „Penaokurve“ können aber Flächen beliebig dicht zudecken. und man kann sinnvoll den Inhalt der durch sie so "zugedeckten" Fläche messen. Etwa beim Kreis lernt jeder Schüler kennen, wie man durch Auszählen immer feinerer die Kreisfläche überdeckenden Quadrate den Flächeninhalt als Grenzwert beliebig genau abschät-zen kann. Versuchen wir nun, auch einen Flächeninhalt der Schneeflockenkurve abzuschätzen, indem man geeignet beliebig feine Quadrate darüber legt und den Grenzwert der Summe der Inhalte dieser Überdeckungsquadrate bestimmt. 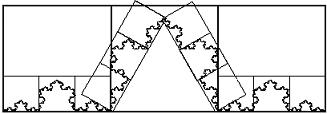Abb. 3 Ausmessen durch Abdeckung mit Flächen In Abbildung 3 ist die Konstruktion dieser Überdeckung mit Quadraten dargestellt. Man erkennt drei größere, an der Grundlinie der Länge 1 nebeneinander gelegte Quadrate der Kantenlänge 1/3, die die Schneeflockenkurve überdecken. Sie überdecken die Schneeflockenkurve und der Flächeninhalt der gesamten Schneeflockenkurve müßte also kleiner als der dieser drei Quadrate sein. Er ist A(0) = 3 x (1/3)^2 = 1/3 [FE] sein (FE steht für Flächeneinheit). Schon etwas besser kann man die fragliche Fläche der Schneeflockenkurve mit Quadraten der Kantenlänge 1/9 mit dem Inhalt (1/9)^2 = (1/81) abschätzen. Man erkennt, dass sich die ganze Kurve aus vier kleinere Kurvenstücke zusammensetzt, die exakte um den Faktor 1/3 verkleinerte Kopien der ganzen Kurve sind. Diese vier Teilstücke werden im kleinen mit Quadraten der Kantenlänge 1/9 genauso überdeckt wie zuvor das ganze Kurvenstück. Aus A(0) = 1/3 wird dann A(1) = 4 × 3 × (1/9)^2 = (1/3) × (4/9) = A(0) × (4/9) [FE]. Ähnlich erhält man beim Überdecken mit Quadraten der Kantenlänge 1/27: A(2) = A(1) × (4/9) = A(0) × (4/9)^2 [FE]. Bei immer weiteren Überdeckungen mit immer kleineren Quadraten der Kantenlänge (1/3)^n erhält man also A(n) = A(0) × (4/9)^n [FE]. Der Gesamtinhalt dieser die Schneeflockenkurve vollständig "zudeckende" Inhalt wird mit wachsendem beliebig klein. Ein Flächeninhalt der Schneeflockenkurve kann nicht größer als dieser Wert sein, ist damit also genau Null. Zum Anfang 3. Das Messen ist zweimal gescheitert! Nun eine Lösung, ein passender Messversuch: Die beiden herkömmlichen Methoden der Längen- und Flächenmessung versagen bei der Schneeflockenkurve. Die eine ergibt zuviel (jedes Mal Unendlich!), die andere zu wenig (je-des Mal Null), um sinnvoll zu messen. Trotzdem bleibt unsere Frage bestehen. Die beiden Teilstücke in Abb. 3 sind offensichtlich verschieden groß. Wie kann man sie sinnvoll quantitativ vergleichen? Gibt es eine Alternative zur herkömmlichen Längen- oder Flächenmessung? Während in vielen Beiträgen an dieser Stelle jedes wirkliche Messen meist aufgegeben und allenfalls die fraktale Dimension bestimmt wird, suchen wir weiter nach einer Alternativen. Dabei kommen wir mathematisch näher an das sogenannte Hausdorffmaß mit seinen Ursprüngen bei Felix Hausdorff. Die Lösung! Eine neue Maßeinheit muss her: Das Schneeflockenmeter Als erstes seien Grundlagen des Messens reflektiert: Zum Messen eine Gegenstandes braucht man immer zwei, einer von zu bestimmender Größe, und ein anderer, mit dem er verglichen (= gemessen) wird. Es gelten die Grundsätze allen Messens: 1. Zwei zerlegungsgleiche Figuren haben gleiches Maß. (Zerlegungsgleich heißt: Es gibt eine Zerlegung der einen in solche Teilstücke, mit denen man die andere ohne Lücken und Überscheidungen auslegen kann. Insbesondere sind zwei kongruente Figuren sind inhaltsgleich.) F zlgsgl G à M(F) = M(G) 2. Wenn ich eine Figur in zwei Teile zerlege, dann ist der Inhalt der Gesamtfigur gleich der Summe des Inhalts der beiden Teilfiguren. M(F u G) = M(F) + M(G), wenn F d G = {} Zur vollständigen Einführung eines Maßes in einem System von Figuren gehört eine Maßein-heit(Maßstab). Eine Figur aus dem System muss zur Bildung deiner solchen Maßeinheit ausgewählt werden. Von den anderen Figuren wird „gemessen“, indem man zählt, in wieviel Exemplare dieser ausgewählten Maßfigur sie zerlegt werden kann. Der Inhalt dieser Maßfigur erhält das Maß 1 und ist die Maßeinheit beim Arbeiten mit dem betr. Größenbereich. Beispiele: B1) Die Maßfigur der Längen ist die Meterstrecke, also jede Strecke, die gleichlang zum Urmeter in Paris ist. Ihre Länge heißt 1 Meter (kurz: 1 m) und ist Einheit für Längen. B2) Die Maßfigur für Flächeninhalte ist ein „Meterquadrat“ - das sei ein Quadrat mit den Kantenlängen 1m. Es hat den Flächeninhalt 1 Quadratmeter (kurz: 1 qm bzw. 1 m2 usw.). Letzteres ist die Einheit der Flächenmessung. Wenn die gewählte Maßeinheit in der Praxis zu grob ist, kann man kleinere daraus ableiten. Und wenn (wie bei der Meterstrecke, dem Meterquadrat, dem Meterwürfel) eine Maßfigur in verkleinerte Kopien ihrer selbst zerlegbar ist, geht das besonders gut. Beispiel: Der Inhalt eines „Dezimeterquadrates“ (das sei ein Quadrat der Kantenlänge 1 dm) ist der 100te Teil des Quadratmeters, da sich ein Meterquadrat in 100 Dezimeterquadrate zerlegen läßt. Kurz: 1 dm2 = 1/100 m2. (Bei einem "Meterkreis" etwa als alternativer Maßeinheit für Flächeninhalte wäre eine Zerlegung in kleinere Einheiten so nicht möglich!) Diese abgeleiteten Maßeinheiten haben lediglich praktischen Nutzen sind aber prinzipiell ent-behrlich. Für das Messen von Schneeflockenkurven suchen wir nun eine geeignete Maßfigur, deren Inhalt dann die Maßeinheit ist. Eigentlich ist das gar nicht so schwierig, diese zu finden. Wenn man sich überlegt, daß bei den Flächeninhalten ein Quadrat mit den Seitenlängen 1 m als Maßfigur dient und bei Volumina ein Maßwürfel mit den Kantenlängen 1 m, so könnte bei den Schneeflockenkurveninhalten eine Schneeflockenkurve mit der Grundseitenlänge 1 m gewählt werden, also die Schneeflockengrenzfigur F¥, die entsteht, wenn die Schneeflockenkonstruktion auf eine Ausgangsstrecke von der Länge 1 m angewendet wird. Diese Meter-schneeflockenkurve und alle zu ihr kongruenten und zerlegungsgleichen Figuren haben den Inhalt 1 Schneeflockenmeter = 1 Sm. 1 Sm sei die Maßeinheit für die Schneeflockeninhalte. Der Einfachheit halber werde das Repräsentantensystem (= System der zu messenden Schneeflockenkurven) auf diese „Urschneeflockenkurve“, auf alle Teilstücke und auf neue abzählba-ren Zusammensetzungen davon beschränkt. Es sei als S1 bezeichnet. Im folgenden Abschnitt wird demonstriert, wie der Inhalt von beliebigen Teilstücken der Meterschneeflockenkurve ausgemessen werden kann. Wie sich zeigen wird, kommen in diesem einfach erscheinende System auch schon inkommensurable Figuren vor, das sind solche, deren Inhalt man nicht mit endlich vielen Bruchteilen der Maßeinheit erfassen kann (wie die Länge der Diagonale des Einheitsquadrates im System der Strecken). Es wird also auch mit unendlichen Zerlegungen zu arbeiten sein. Zum Schluß noch zwei Anmerkungen: Wie bei den alltäglichen Größenbereichen gewohnt, kann man auch kleinere Maßeinheiten ableiten, allerdings nicht passend zum Zehnersystem was bei Strecken, Flächen und Volumen wegen der Selbstähnlichkeit mit dem möglichen Streckfaktor k = 10 sondern wegen des Streckfaktors 3 im Dreiersystem. Ein Dezimeterquadrat hat die Maßeinheit 1 Quadratdezime-ter = 1dm^2, 1 dm^2 = 1/100 m^2. Eine Drittelmeterschneeflockenkurve hat die Maßeinheit 1 Schneeflockendrittelmeter = 1 Sdrm. 1 Sdrm = 1/4 Sm, denn die Meterschneeflockenkurve läßt sich in vier Drittelmeterkurven zerlegen. Entsprechen hat die Neuntelmeterkurve die Maßeinheit Schneeflockenneuntelmeter = 1 Snem und 1 Snem = 1/16 Sm. Weiter sei darauf hingewiesen, daß das so gewählte System von Schneeflockenkurven stark eingeschränkt ist. Es fehlen mangels endlicher oder abzählbarer Zerlegungsgleichheit z.B. die Halbmeter-, die Viertelmeter-, Dezimetermeterschneeflockenkurve. Auf die Einbeziehung dieser verkleinerten Kopien der Meterschneeflockenkurve wird im Abschnitt 5 eingegangen. Zum Anfang 4 Protokolle als Messgehilfen Test Es gilt nun, den Inhalt eines Teilstückes zwischen zwei beliebigen Punkten der Meterschnee-flockenkurve auszumessen. Nachzulesen in W. Sternemann 1998 IPN Kiel.) (Letztlich wird ein solches Teilstück durch höchstens abzählbar viele verkleinerte Kopien der Meterschneeflocke und deren Zusammenfassungen("Bündelungen") ausgemessen. Die Maßzahlen kann man direkt in endliche oder unendlichen 4-adischen Brüche übersetzen. Jeder 4-adische Bruch hat dem entsprechend höchstens abzählbar viele Ziffern. Zum Anfang 5 Selbstähnlichkeitsdimension und Schneeflockeninhalt Die fraktale Dimension D = log(4)/log(3) de Schneeflockenkurve ergibt sich bekanntlich aus der strengen Selbstähnlichkeit. In der Schule begründet man diese seltsame Dimension ge-wöhnlich nach folgendem Schema: · Die Selbstähnlichkeit wird festgestellt. Sie besagt in diesem Fall, daß die Figur genau aus vier um den Faktor 1/3 gestauchten Kopien ihrer selbst besteht. Oder umgekehrt gesagt: Man erhält 4 Schneeflockenkurven, wenn man eine um den Faktor 3 zentrisch streckt. · Dies wird verglichen mit schon vertrauten Figuren, die sich für die Schüler überraschend auch als selbstähnlich erweisen. Rechteck, Parallelogramm, Dreieck, u.a. Flächen wie auch Quader, Tetraeder, u.a. Körper, wo man jedesmal die mit geeignet gewähltem Faktor k ge-streckte Figur in eine Anzahl f von Kopien zerlegen kann. · Bei diesen vertrauten Flächen und Körpern „entdeckt“ man eine Beziehung zwischen f und k: f = k2 bei Flächen und f = k3 bei Körpern. Eine Streckung um den Faktor k bewirkt also eine Vervielfachung um kD , wobei D mit 2 oder 3 die Dimension der Figur ist. Das läßt sich sogar auf Strecken erweitern, da diese auch selbstähnlich sind. Dieser Zusammenhang stellt sich von der zentrischen Streckung her als aus der Mittelstufe bekannt heraus. Dort war k nicht nur ein geeignet zu wählender sondern ein beliebiger positiver reeller Streck-faktor, und f keine Anzahl sondern der reelle Faktor, um den der Flächeninhalt bzw. das Volumen wuchs. · Dieser Zusammenhang wird formal auf die Schneeflockenkurve übertragen. Sucht man auch hier anstelle der Exponenten 2 und 3 im Vervielfachungsfaktor nach einem passenden neuen Exponenten D, so führt das zu 4 = 3D bzw. D = log(4)/log(3). Bei dieser Einführung als Selbstähnlichkeitsdimension wird die fraktale Dimension gegen-über dem Schüler allein als Vervielfachungsexponent beim Strecken um den Faktor 3 begrün-det. Zum einen stört dabei, daß diese Definition streng genommen allein für die streng selbstähnli-che, auf einer Strecke konstruierte spezielle Schneeflockenkurve gilt. Nicht für die Teilfiguren und nicht für zusammengesetzte Schneeflockenkurven wie die „Küste“ der Schneeflockenin-sel u.a. Man dehnt dann intuitiv, aber ohne mathematische Begründung den gewohnheitsmä-ßig weiter benutzten Begriff der Dimension auf alle anderen Schneeflockenkurvenfiguren aus. Zum anderen wirkt es sehr künstlich, daß das Strecken auf die Wahl von k = 3 mit zugehöri-gem f = 4 beschränkt ist. Bei den selbstähnlichen Flächen und Körpern war k Î N wählbar und erweiterbar auf beliebiges k Î R, wenn man von den zu zählenden Figurenkopien zu den entsprechenden Inhalten überging. Auch die sich bei Mehrfachstreckung ergebende mögliche Ausweitung der einzigen Wahl von k = 3 auf unendlich viele mit k = 3n n Î N, überzeugt nicht wirklich sondern läßt die fraktale Dimension der Schneeflockenkurve weiterhin eher als etwas künstliches erscheinen. Mit dem hier entwickelten Schneeflockeninhalt als Stütze kann man beide störenden Aspekte mildern bzw. beseitigen. Erstens kann man nachrechnen, daß für alle Repräsentanten unseres Schneeflockenfigurensystems gilt: Streckung um den Faktor 3 vervielfacht den Schneeflo-ckeninhalt um 4. Die Gleichung 4 = 3D bezieht sich also auf die Inhaltszunahme auch der nichtselbstähnlichen Schneeflockenkurven. D ist damit Wachstumsexponent des Inhalts beim Strecken um den Faktor k = 3. Zweitens kann man auch die störende Einschränkung auf k = 3 zumindest abmildern. Prob-lemlos ist die Erweiterung auf k = 3z, z Î Z. , indem man mehrfach vorwärts und rückwärts streckt. Der Faktor f der Inhaltszunahme zum Strecken um k = 3z ist dann offensichtlich f = 4z = (3D)z = (3z)D = kD. Dies gilt für alle, auch die nichtselbstähnlichen Figuren unseres Reprä-sentantensystems. Eine Erweiterung dieses Ansatzes auf beliebiges k Î R wie bei Linien, Flä-chen und Körpern erfordert andere Methoden des Zerlegens bzw. „Ausmessens“, nämlich die von F. Hausdorff für seine heute nach ihm benannten „Hausdorffdimension“ benutzten belie-bigen, offenen, höchstens abzählbaren, „beliebig feinen“ Überdeckungen. Es wäre zu prüfen, ob es, um die schwierige Definition des Hausdorffmaßes zu umgehen, für die Schule nicht wohldefiniert und widerspruchsfrei möglich ist, für beliebige k den Inhalt einer um k gestreckten Figur F’ einfach per Definition auf den Inhalt der Ausgangsfigur F zurückzuführen indem man I(F’) =Df kD ×I(F) mit D = log(4)/log(3) setzt. Ist S1 das zuvor zugrundegelegte Repräsentantensystem aller zur Meterschneeflocken-kurve gehörenden Schneeflockenkurven, dann ist mit dieser Definition das System der meßba-ren Schneeflockenkurven auf S = {k×M½ k Î R, M Î S1} ausgeweitet. S ist groß genug, um alle spontan vorstellbaren Schneeflockengebilde zu erfassen. Zum Anfang 6 Schluß Es ist fast selbstverständlich, daß diese Überlegungen exemplarisch sind und nicht nur für Schneeflockenkurven durchführbar sind. Analog kann man mit anderen Figurensystemen aus Cantormengen, Sierpinksidreiecken, u.a. verfahren. Mit der hier ausgeführten Interpretation der fraktalen Dimension als „Wachstumsexponent eines zugehörigen Inhalts beim Strecken“ trifft man einen wesentlichen Aspekt der Fraktale. Sie ist für Schüler nachvollziehbar und einsichtig. Die intuitiven Zusatzdeutungen wie „Maß für Komplexität“ oder „Verfranstheit“, „Filigranität“, „Zerklüftetheit“ usw. empfehlen sich weniger, da die Definition der gebrochenen Dimension sie nicht her gibt. Die Erfahrung zeigt, daß diese Deutungen immer wieder durch Gegenbeispiele relativiert bzw. in Frage gestellt werden müssen. Die Deutung als Wachstumsexponent des Inhalts beim Strecken um den Fak-tor k hat den Vorteil, daß sie in allen Fällen zutrifft. Felix Hausdorff führte 1919 in der bekannten Arbeit mit der heute nach ihm benannten „Hausdorff-Dimension“ den mathematisch tragfähigsten Begriff einer gebrochenen Dimensi-on ein. Schon er stellt dort zu seiner komplizierten nur zusammen mit einem Maß definierten Dimension genau die Eigenschaft als Wachstumsexponent fest: „ ... Wenn überdies L(B) = mp × L(A) ist sobald B zu a im Verhältnis m : 1 ähnlich ist, so nen-nen wir L ein äußeres Maß der Dimension p. ...“, (Hausdorff 1919 S. 158) Falconer schreibt in dem Lehrbuch „Fractal Geometry“ : „ ... On magnification by the factor l ... the volume of a 3-dimensional object is multiplied with l3. As might be anticipated, s-dimensional hausdorff measure scales with the factor ls ... Such scaling properties are fundamental to the theory of fractals. ...“, zusätzlich die fundamentale Bedeutung dieser eigen-schaft betonend. (Falconer. 1990, S. 26) Hausdorff ging es allerdings primär nicht um eine neue Dimension sondern um ein neues Maß, er sprach von einem „p-dimensionalen Maß“ und erwähnte dabei eher implizit auch eine neue Dimension. Überhaupt wird der in diesem Beitrag vertretene Standpunkt, die fraktale Dimension in engem Zusammenhang mit dem Messen zu sehen, schon dadurch bestärkt, daß mathematisch und mathematikgeschichtlich die gebrochene Dimension nur zusammen mit einem zugehörigen Maß auftritt. Sie war ursprünglich ein Hilfsmittel für ein neues Maß, eher ein Nebenprodukt. Hausdorffs Bezeichnungen für diese Dimensionszahl wie „Graduierungsmerkmale“, „Ord-nung des Nullwerdens“, „Stärke der Konvergenz“ oder „Konvergenzexponent“ belegen das (Hausdorff 1919 S. 157). Im vorliegenden Beitrag ging es um einen Elementarisierungsversuch des Dimensionsbegriffs auf dem Level der Schulmathematik. Ein ergänzender und m. E. näher an der Hausdorffdi-mension liegender Versuch, die fraktale Dimension als Meßbarkeitsexponent auch bei nichtselbstähnlichen Fraktalen zu verstehen, wird in (Sternemann 1995.1, Kapitel 5) versucht.. Zum Anfang Literatur von Koch, Helge"Sur une courbe continue sans tangente, obtenue par une constuction géometrique élémentaire", Arkiv för Matematik 1 (1904), 681-704 W. Sternemann. Das "Schneeflockenmeter". Ein Denkanstoß zum Messen von Schneeflockenkurven. In M. Komorek/ R. Duit/ M. Schnegelberger (Hrsg.), Fraktale im Unterricht IPN-Materialien Kiel 1998 Anmerkungen: 1) Dieses Dokument ist eine veränderte Fassung eines vor einigen Jahren erschienen Aufsatzes mit gleichem Titel (Siehe oben unter Literatur!). Diskussionen darüber sind willkommen. Email: sternemann(at)t-online.de 2) F(unendl) ist lediglich eine Sprechweise genauso wie "unendlich oft iterieren". Letztlich ist damit lediglich die Grenzfigur gemeint, deren Punkte in der Ebene eindeutig festliegen und von der die Iterationsfiguren F(n) mit wachsendem n beliebig wenig unterscheidbar sind. Zum Anfang