2. Aktuelle Experimente
mit "Platonischen Fraktalen" in der Schule
Vorbemerkung
2.1.
Die Konstruktionsvorschrift (Entstehung und Präzisierung)
Die
Frage, Eine
Konstruktionsvorschrift
2.2. Anwendung auf ebene
reguläre Polyeder
2.3. Anwendung auf das
Oktaeder
2.4. Anwendung auf
das Ikosaeder
2.5. Anwendung auf
das Dodekaeder
2.6.
Angaben zur konkreten Herstellung unserer Modelle
2.7. Ausblicke
auf weitere Möglichkeiten zu mathematischen Experimenten
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen
2. Experimente mit platonischen Fraktalen in unserem Unterricht:
Vorbemerkung
Was haben diese seltsamen mathematischen Monster in der Schule zu suchen?
Wir haben im Mathematikunterricht doch wahrlich genug Probleme und
Krisen zu bestehen. Und es ist noch offen, ob der Tiefpunkt schon erreicht
ist.
Ich glaube daß mit den platonischen Fraktalen kleine Inseln aufgezeigt werden, wo Mathematik ein bischen Spaß gemacht hat. Auch werden für den Bereich der Facharbeiten in diesem Vortrag eine Reihe von Anregungen stecken.
In meinem Unterricht kommen Fraktale zum einen im Differenzierungsunterricht
der Jahrgangsstufe 10, zum andern im Mathematikleistungskurs der
Jahrgangstufe 13 und des weiteren in einer freiwilligen Arbeitsgemeinschaft
vor.
In den ersten beiden Fällen (= Pflichtunterricht) sind die Fraktale
und die gebrochene Dimension fester Unterrichtsbestandteil und zwar mathematisch
in dem Sinne, wie oben beschrieben, allerdings ziemlich kurz und eher am
Rande als geometrische Ergänzung zu dem Hauptgegenstand Iterationen.(Siehe
Bemerkung!)
Aber an dieser Stelle sind nicht die Iterationen sondern platonische
Fraktale unser Thema. Sie Fraktale gehören zum Verständnis der
Iterationen dazu. Im o. g. Pflichtunterricht werden sie gezeichnet und
zu vorgegebenen Figuren ihre gebrochene Dimension berechnet
Auch wenn sie meist keine direkt sichtbaren Anwendungen zu haben scheinen,
gibt es es zu den Fraktalen eine sehr große Fangemeinde, sichtbar
auch im Internet in Form von unzähligen exotisch schönen Bildergallerien.
Außerhalb des Pflichtunterrichts gab es bei uns immer eine kleine
Gruppe von Schülern, die Spaß daran hatten in kleinen QBASIC
oder PASCAL-Programmen Bilder zu produzieren. Leider werden solche Schüler
zur Zeit seltener.
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen
Bei der Beschäftigung mit den beiden klassischen räumlichen Fraktalen Sierpinskitetraeder und Mengerschwamm im Differenzierungsunterricht entstand
Die Frage:
Würfel und Tetraeder sind platonische Körper! Sie haben beide ihr klassisches Fraktal.
Was ist mit Oktaeder, Ikosaeder und Dodekaeder?
Frage:
Wie sehen in Anlehung an Sierpinskitetraeder und
Mengerschwamm die Fraktale zu Oktaeder, Dodekaeder und Ikosaeder aus?
Trotz intensiver Bemühungen von Schüler und Lehrer war keine Literatur zu finden! (Siehe Anmerkung!)
Also war die spannende Idee geboren, selbst etwas zu erfinden. Schwer
konnte das doch nicht sein. Trotzdem auch nicht trivial.
Die vage Vorstellung eines platonischen Fraktals in Anlehung an Sierpinskitetraeder
und Mengerschwamm mußte präzisiert werden!
Selbstähnlich sollte die Figur werden!
Sie sollte aus lauter verkleinerten Oktaeder, Ikosaedern Dodekaedern
usw bestehen.
Die Frage galt der Suche nach einer Konstruktionsvorschrift für Fraktale aus Oktaeder, Ikosaeder und Dodekaeder, und zwar möglichst so einfach wie die beiden vorhandenen zu Tetraeder und Würfel. Zugegeben war es doch der Lehrer, der hierüber weiter nachgrübelte.
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen
Die erstaunlich einfache Konstruktionsvorschrift:
Die Vorschrift bei Menger lautet sinngemäß: "Entferne von
einem Würfel die inneren sieben der siebenundzwanzig Drittelwürfel
und wiederhole das mit jedem der zwanzig nicht entfernten Würfel.
...".
Eine Vorschrift in dieser Art ist für unseren Zweck ungeeignet
und von den fünf platonischen Körpern nur bei dem ( streng selbstähnlichen
) Würfel möglich.
Denn wenn man aus einem Oktaeder kleinere Oktaeder entfernt, so ist
der Rest keine Figur aus Oktaedern mehr. Entsprechendes gilt für Ikosaeder,
Dodekaeder und auch schon für das Tetraeder! Beim Sierpinski-Tetraeder
wurden keine Tetraeder entfernt sondern Tetraeder an den Ecken stehen gelassen.
Entfernt wurde im Innern dazu der Rest. Und der ist bekanntlich ein Oktaeder.
Wichtiger als das, was weggenommen wird, ist also das, was in der Figur
bleibt.
Eine Formulierung der Vorschrift zu Sierpinski's Konstruktion aus dieser Sicht lautet: "Lasse von einem Tetraeder an jeder Ecke je ein halb so großes Tetraeder stehen und entferne den Rest und wiederhole das mit jedem entstandenen Tetraeder.... ". Diese Vorschrift läßt sich offensichtlich besser auf alle anderen platonischen Körper übertragen. Lediglich die Größe der verkleinerten Figuren an den Ecken ist offensichtlich flexibler als "halb so groß" zu wählen. So kommen wir zur endgültigen
Konstruktionsvorschrift zu Fraktalen aus einem Poyeder:
"Lasse von einem Polyeder an jeder Ecke möglichst
groß je eine gleichgroße Verkleinerung in paralleler Lage stehen
und entferne den Rest. Wiederhole dies mit jedem entstandenen verkleinerten
Polyeder.... ".
Möglichst groß heißt, daß die gleich großen verkleinerten Figuren sich also gerade berühren aber nirgends überschneiden.
Diese Vorschrift ist so einfach, daß man sich wundert, daß sie in der Literatur noch nicht zu finden ist! Sie führt zwingend zu einer Lösung, auch übrigens bei anderen nichtregulären Polyedern mit der Möglichkeit zu interessanten mathematischen Experimenten.
Dabei interessieren die z.B. folgende Fragen:
- Wie berühren sich die verkleinerten Figuren im ersten Iterationsschritt
? Beim Sierpinski-Tetraeder berührten sich die vier kleinen Tetraeder
in Punkten. Sie könnten sich auch an Kanten oder auf ganzen Flächen
berühren?
- In welchem Maßstab steht die verkleinerte Figur zur ganzen
Figur? Denn aus diesem Verkleinerungsfaktor errechnet sich u.a. die fraktale
Dimension bzw. Hausdorffdimension!
- Wie sieht die topologische Dimension der Grenzfigur aus? Sierpinski-Tetraeder
und Mengerwürfel sind Kurven, also Liniengebilde mit der topologischen
Dimension 1.
- Beim Tetraeder ist die freigebliebene Lücke ein Oktaeder. Wie
kann man die entstandenen Lücken beschreiben?
- Gibt es interessante Schnittflächen?
usw.
Wenn wir im folgenden die oben entwickelte Konstruktionsvorschrift anwenden, so werden wir einige dieser Fragen beantworten. Es werden für den Leser aber sicherlich genügend unbeantwortete Fragen für Eigenexperimente offen bleiben. Experimentieren läßt sich auch sehr gut mit Abwandlungen dieser Konstruktionsvorschrift!
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen
Anwendung auf die regelmäßigen
Vielecke
Auch weil wir auf diese unten zurückgreifen müssen, sei die
analoge Vorgehensweise in der Ebene für regelmäßige Vielecke
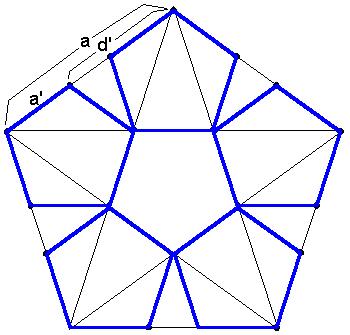
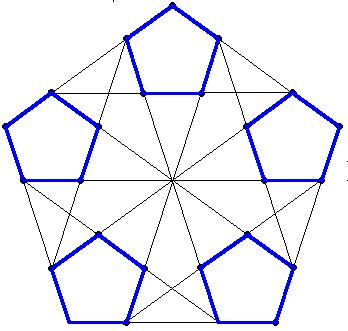
insbesondere beim Fünfeck demonstriert.
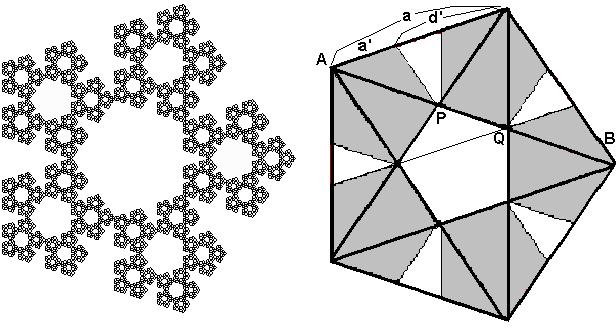
d/d' = a/a' = 1 + phi
Anwendung beim regulären 5-Eck
Die linke fraktale Figur zum Fünfeck wird auch gelegentlich auch Dürerfünfeck genannt. Weiß jemand, wie es zu dieser Bezeichnung kommt?
Solche "Eckenteppiche" erhält man zu jeder Eckenzahl. Beim Sechseckteppich
erkennt man als Berandung genau die bekannte Kochkurve, bzw. Schneeflockenkurve.
Bei größer werdender Eckenzahl (Siehe 11-Eck ) läßt
sich die Figur immer weniger von einem Kreis unterscheiden.

Anwendung beim regulären 6-Eck
Anwendung beim regulären 11-Eck
Zwei Verkleinerungen berühren sich in diesen Abbildungen immer
in einem Eckpunkt. Es sei angemerkt, daß sich beim Achteck, beim
12-Eck und in vielen anderen Fällen die Figuren an ganzen Kanten
berühren.
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen
Anwendung der Konstruktionsvorschrift
auf das Oktaeder:
 |
 |
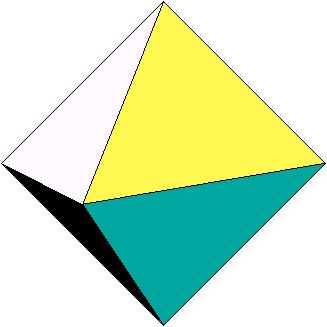
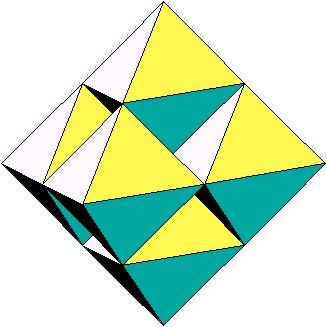
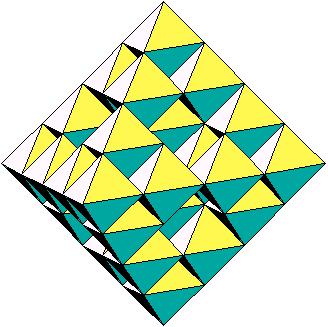
Sechs verkleinerte Oktaeder an den Ecken in paralleler Lage. Sie berühren
sich an ganzen Kanten.
 |
 |
 |
 |
|
|
Iterationsstufe 0 |
Iterationsstufe 1 |
Iterationsstufe 2 |
Iterationsstufe 3 |
|
erklären sich selbst. Die Grenzfigur, die hier entsteht, sei in
Anlehnung an die von Mandelbrot stammende Bezeichnung "Mengerschwamm" als
"Oktaederschwamm" bezeichnet. Einen Oktaederschwamm zu konstruieren,
ist erstaunlich einfach!
Anders als beim Tetraeder berühren sich die sechs verkleinerten
Oktaeder an ganzen Kanten. Einen Eckpunkt haben sie sogar alle sechs im
Mittelpunkt der Figur gemeinsam. Als Maßstab ergibt sich 2 : 1, derselbe
wie beim Tetraeder. Damit passen die sechs Oktaeder verblüffend gut
zusammen und weggenommen wurden acht Tetraeder. Das in einem Schritt
verringerte Volumen ist 6/8 = 62,5% des vorherigen Volumens. Beim
war das 4/8 = 50%
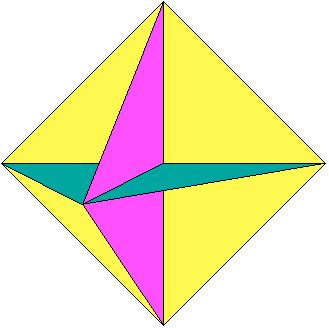
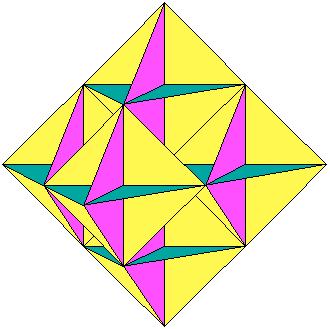
Die Hauptüberraschung des Oktaederschwamms folgt aber noch: In der nachfolgenden Abbildung sind die drei inneren Diagonalflächen der auftretenden Oktaeder gezeichnet und auch die in den nachfolgenden Iterationsfiguren.
Die inneren Diagonalflächen in den ersten Iterationsfiguren zum Oktaederschwamm:
 |
 |
 |
|
Iterationsstufe 0 |
Iterationsstufe 1 |
Iterationsstufe 2 |
Es ist offensichtlich so, daß diese Flächen in jedem Oktaeder
beim Entfernen der nächsten acht Tetraeder voll erhalten bleiben.
Faßt man die Folge dieser Flächenfiguren als eigene Iteration
auf, so ist sie in dem folgenden Sinne umgekehrt: Statt Schrumpfen durch
Entfernen von Volumenelementen hat man das Wachsen durch Hinzufügen
von Flächen. Dieser wachsende immer feiner werdenden Fächer aus
Flächen hat die gleiche Grenzfigur wie der immer weiter durchlöcherte
schrumpfende Oktaederkörper der vorherigen Iteration.
Damit ist klar, daß die Grenzfigur mindestens ein flächiges Gebilde ist, daß sie die topologische Dimension 2 hat! Der topologische Beweis, daß sie nicht drei ist, sei an dieser Stelle anderen überlassen. Durch diese Eigenschaft unterscheidet sich der Oktaederschwamm stark von dem Sierpinski-Tetraeder und Mengerschwamm welche beides Liniengebilde sind, Figuren mit der topologischen Dimension 1.
Topologen können die Frage stellen, ob diese neuen Figur auch Universalitätseigenschaften
wie Sierpinski-Tetraeder oder Mengerschwamm haben, ob er als eine Art Universalfächer
angesehen werden kann für einen Bereich an flächigen Figuren,
die dann alle als Teilfigur homöomorph im Oktaederschwamm stecken
müssen. Die Frage läßt sich weiterspinnen: Wie ist das
bei dem Oktaederschwamm, der beim Dritteln der Kantenlängen entsteht?
Der ist insofern komplexer, weil in ihm im Innern unendlich viele eingeschlossen
räumliche Kammern entstehen. Wir brechen an dieser Stelle die Kette
der Fragen ab, denn die beiden anderen Schwämme, der Ikosaeder und
Dodekaederschwamm haben auch ihre interessanten Aspekte.
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen
Ikosaeder
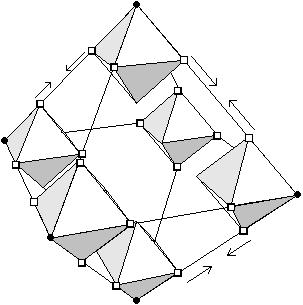
Anwendung der Konstruktionsvorschrift auf den Ikosaeder
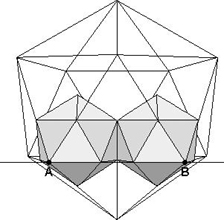
Wie stoßen zwei benachbarte Ikosaeder aneinander?
Im Bild sieht man zwei kleine Ikosaeder, die nebeneinander in paralleler Lage gemeinsam an einer Kante des Ausgangsikosaeders hängen. Man erkennt im Bild, daß sich die zu AB senkrechten Kanten genau berühren müssen. Wie beim Oktaeder berühren sich zwei verkleinerte Ikosaeder an einer ganzen Kante.
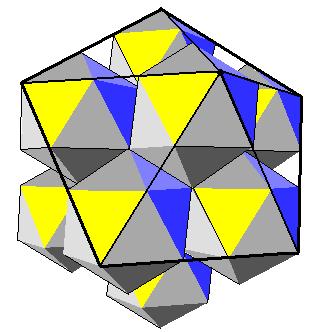
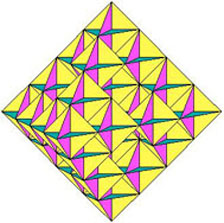
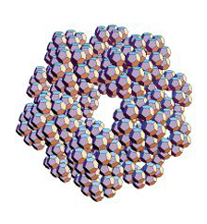
Es entsteht ein neues, interessantes, überraschend kompaktes, in
der Literatur nicht zu findendes Kluster von 12 Ikosaedern.
Die drei Schülerinnen Maike Mevenkamp, Caroline Schenk und Janina
Schlenkert Klasse 10 des Gymnasium Canisianum Lüdinghausen waren zur
großen Freude des Verfassers dazu bereit, die ersten beiden Iterationsfiguren
aus Papier herzustellen.
Es entstand eine ästhetische Figur, deren Schönheit und Anschaulichkeit
durch keine Computergrafik zu ersetzen ist.

Foto des Knubbels und der Hersteller siehe Spektrum der Wissenschaft November 2000, oder hier.
Der Verkleinerungsmassstab:
Fragen wir uns nun nach dem Maßstab a : a'. Die Berechnung der
Streckenlängen über die Koordinaten der Eckpunkte mit Hilfe der
analytischen Geometrie erwies sich als sehr aufwendig. Wir kamen auf Systeme
von mehreren nichtlinearen Gleichungen mit entsprechend vielen Unbekannten.
Auch Software wie DERIVE verhalf uns nicht zu klaren Lösungen. Irgendwann
fiel dann der Blick auf eine besondere Schnittfläche.
Die Hausdorffdimension ist damit log(12) / log(2,618...) = 2,58193... , stimmt also sogar bis auf zwei Dezimalen mit der vom Oktaederschwamm log(6) / log(2) ? 2,5849625... überein.
Schaut man auf eine Kante, so wird sie durch die Iteration immer wieder in Stücke zerteilt und in einen Cantorstaub verwandelt. Die Stücke bleiben aber durch hinzukommende Streckenzüge immer wieder neu als ein Liniennetz miteinander verbunden. Die topologische Dimensionen Ikosaederschwamms ist also 1 und wesentlich von der des Oktaederschwamms verschieden. Ein Beweis für diese topologische Dimension steht allerdings noch aus und erfordert Spezialkenntnisse aus der Topologie.
Interessant ist auch die Restfigur, die aus einem Ikosaeder in einem
Iterationsschritt entfernt wird. Außen wird unter jeder Kantenmitte
ein nicht ganz reguläres Tetraeder (fünf Kanten der Länge
a' und eine von a'/Phi) entfernt und unter jeder Flächenmitte eine
sechsseitige Pyramide ( 9 Kanten der Länge a' und drei der Länge
a'/Phi). Im Innern in der Mitte wird im ersten Iterationsschritt ein geschlossener
Raum geleert, der die Form eines Dodekaeders hat, bei dem dann zusätzlich
an jeder der 12 Flächen eine fünfseitige nach innen gerichtete
Pyramide weggenommen wird, so daß ein nichtkonvexer Hohlraum vorliegt,
der von 12 x 5 = 60 gleichseitigen Dreiecken mit 90 gleichlangen Kanten
begrenzt wird. Dieser eingeschlossene Innenraum erhält aber sofort
im nächsten Iterationsschritt durch neue Öffnungen Verbindung
nach außen. Je höher die Iterationsstufe, um so größer
werden die Durchblicke, um so lichter wird die Figur. Leider gibt es zur
Zeit noch keine Bilder von ihr.
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen
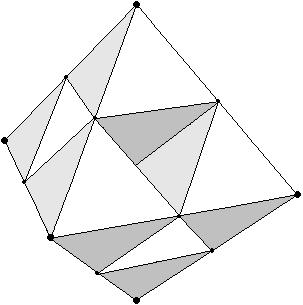
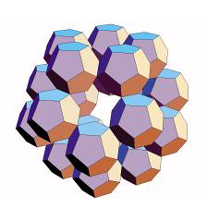
Anwendung der Konstruktionsvorschrift auf das Dodekaeder
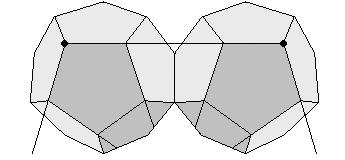
Wie stoßen zwei benachbarte kleine Dodekaeder aneinander?
Auch hier freuten wir uns, daß wieder wie beim Ikosaeder und
Oktaeder und im Gegensatz zum Tetraeder eine Berührung an einer ganzen
Kante stattfindet. Die Berührkanten liegen orthogonal zur Schiebekante.
Es entsteht wiederum eine ästhetische Figur, luftiger und lichter als der erste Iterationsschritt beim Ikosaeder. Dem Herstellen von Papiermodellen und ihrem Zeichnen steht nichts mehr im Wege:
Ein Foto eines Papiermodells der ersten Iterationsstufe, gebastelt von Barbara Schürmann Februar 2000
Bild folgt in Kürze
Weiterhin eine Abbildung von Prof. Dr. Wobik MPI für Plasmaphyisik Greifswald mit Mathematika, Mai 2000.

Die ersten beiden Iterationsstufen erstellt mit Mathematika Oktober 2000 von Dr. Christoph Pöppe, Spektrum der Wissenschaft
Wann, bei welchem Streckfaktor, berühren sich zwei an benachbarte Ecken des Großen gesetzte kleine Dodekaeder?
Wie beim Ikosaeder entdecktman in dieser Figur an mehreren Stellen den
goldenen Schnitt.
Wie beim Ikosaeder tappten wir auch hier lange im Dunkeln und kamen
mit dem Rechnen mit den Koordinaten der Eckpunkte auch mit Computereinsatz
nicht zu schönen Ergebnissen.
Die Lösung ergab sich dann kurz und schnell ganz ohne Computereinsatz
beim Betrachten der Außenflächen eines Papiermodells der ersten
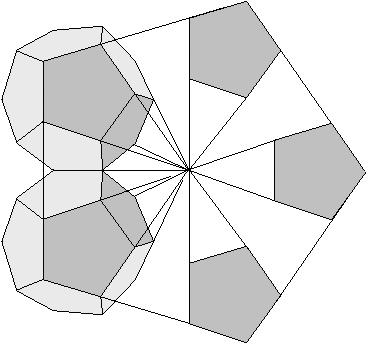
Iterationsstufe. Die fünf kleinen Fünfecken in einem ehemaligen
großen Fünfeck bilden eine dem Dürerfünfeck beim Ikosaeder
ähnliche Pentagrammfigur:
Gab es da vielleicht einen einfachen Zusammenhang! Man suche
nach Symmetrien und auffallenden Eigenschaften! Man wird fündig!
Man entdeckt, daß sich die Verlängerungen der Kanten der
kleinen Fünfecke alle im Mittelpunkt des großen Fünfecks
treffen.
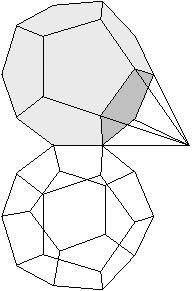
Ein gutes Beispiel ist der Versuch das Ikosaeder aus 20 platonischen Tetraedern zusammenzusetzen. Man kann es fast, die 20 Tetraeder auf den Seitenflächen des Ikosaeders mit der Spitze im Innern sind etwas zu kurz. Der Fehler liegt unter 5%. Meine Schüler hatten einmal ein Ikosaeder aus platonischen Tetraedern gebaut, ohne diesen Fehler wahrzunehmen und glaubten eine Zeit lang felsenfest daran, daß das möglich ist, bis ich sie enttäuschen mußte.
Hier mußte ein zwingender mathematischer Beweis für den gemeinsamen Schnittpunkt im Zentrum gefunden werden. Das ist schwieriger, wenn man Neuland betritt und die Richtigkeit nirgends in der Literatur nachlesen kann
1. Schritt: Man verlängere an einer Seitenfläche die fünf an den Ecken anstoßenden nicht anliegenden Tiefenkanten. Die Verlängerungen treffen sich in einem Punkt. Sie bilden eine Fünfseitige Pyramide. Macht man das an jeder Seite, so erhält man den sogenannten Keplerschen Stern.
2. Schritt: Liegen zwei Dodekaeder an einer Berührkante aneinander,
und gehört die Verlängerung der Berührkante auch zu je einer
solchen Pyramide jedes Dodekaeders, so fallen die Spitzen der kongruenten
Pyramiden aufeinander.
Nachdem diese sehr regelmäßige, dem Pentagramm ähnliche Figur zum Vorschein gekommen ist, konnte das Verhältnis a : a' leicht berechnet werden:
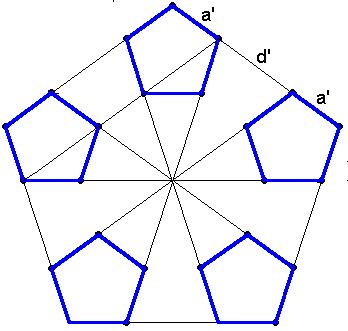
Die Figur steckt voll von harmonischen Verhältnissen. Jede Lücke
zwischen den Fünfecken liegt punktsymmetrisch zu einem Fünfeck,
so daß es praktisch nur zwei Längen in ihr gibt, nämlich
Kantenlänge a' und Diagonalenlänge d' der verkleinerten Fünfecke
bzw. sich alle anderen sich daraus zusammensetzen lassen.
Alle Winkel im Zentrum sind gleich groß.
Bestimmung des Faktors:
die Zahl des Goldenen Schnitts ist.
Damit ergibt sich als Hausdorffdimension der etwas kleinere Wert
log(12) / log(3,618...) 2,32962.... .
Die topologische Dimension der Grenzfigur ist wie beim Ikosaederschwamm
gleich 1. Es handelt sich offensichtlich wie auch schon beim Sierpinskitetraeder
und Mengerschwamm eine Linienfigur. Der Oktaederschwamm war die überraschende
Ausnahme
Eine nette Aufgabe für die Anwendung dynamischer Geometrie-Software, die auch von weniger begeisterten Mathematkern gern gemacht wurde:
Aufgabe:
Konstruiere in einem großen Fünfeck fünf an den Ecken
in paralleler Lage liegende gleich große verkleinerte Fünfecke.
Die Größe der fünf gleichen verkleinerten Fünfecke
soll verschiebbar sein. Beim Verschieben der Kantenlänge der kleinen
Fünfecke fallen automatisch die zwei besonderen Kosntellationen Dürerfünfeck
und Dodekaederfünfeck auf. Hier eine weitere beim Spielen mit einer
Lösung der Aufgabe gewonnene interessante Konstellation: Berechne
auch hierbei den Verkleinerungsmaßstab mit Benutzung der Zahl des
Goldenen Schnitts.
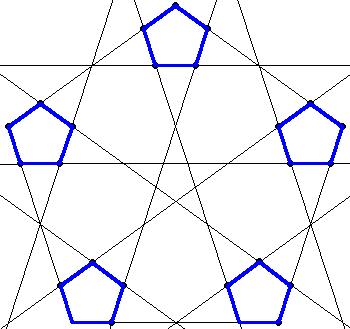
Vielleicht findet man ja noch eine Anwendung dieser Figur in einem ebenen
oder räumlichen Fraktal!?
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen
Konkretere Angaben zur Herstellung der Modelle zu platonischen Fraktalen an unserer Schule
1998
Im Differnzierungsunterricht der 10 wurden Modelle der platonischen
Fraktale hergestellt:
Sierpinskitetraedermodell Iterationsstufe 4 aus Schweißdraht von Bastian Wiedek
Bild wird noch kommen
Mengerschwammmodell Iterationsstufe 2 (durch die vorgegebenen Lochungen wird Iterationsstufe 3 angedeutet) aus 400 blauen Rechenwürfeln aus Plastik von Nicola Kuse
Bild wird noch kommen
Der erste Oktaederschwammmodell Iterationsstufe 4 nach einem Vorschlag
des Fachlehrers.
aus 6^4 = 1296 Plastikkugeln (Industrieabfall der Chemischen Werke
Hüls) in vielen Arbeitsstunden zusammengeklebt von Christoph Kappenberg
.
Bild wird noch kommen
Dazu entstand eine Ausstellung zu Fraktalmodellen in der Pausenhalle der Schule.
Mit dem Oktaederschwamm war damit im Jahre 1998 auch die Konstruktionsvorschrift
zu Ikosaeder und Dodekaeder vorhanden. Es war uns theoretisch klar, daß
sich zwei Ikosaeder und Dodekaeder an einer ganzen Kante berühren
würden. Es gab noch letzte Unsicherheit und vor allem noch kein Modell.
Von Alexander Uth Leistungskurs 12 wurden die Punktkoordinaten von
Dodekaeder berechnet und Rechenversuche zum Verkleinerungsmaßstab
gemacht.
Auch vom Ikosaeder haben wir schließlich mit Pythagoras die Punktkoordinaten als unschöne Rechenterme rausgekriegt. Danach hat der Fachlehrer mit QBASIC kleine Programme geschrieben, welche rekursiv für mehrere Iterationsstufen Kantenmodelle (= "Drahtgestelle") von Ikosaeder- und Dodekaeder-Schwämmen zeichneten, in Zentralperspektive beliebig drehbar und vergrößerbar.
Schließlich fand der Fachlehrer im Internet die elegante Möglichkeit,
die Koordinaten der Eckpunkte von Dodekaeder und Ikosaeder durch die Zahl
des Goldenen Schnitts auszudrücken, was die Programmierung wesentlich
erleichterte.
1999
Frühjahr/Sommer Johannes Rheinländer hat QBASIC-Software
gestrickt, womit alle fünf platonischen (Ecken-) Fraktale mit
gefärbten Flächen gezeichnet werden.
Im Herbst 1999 wurden platonische Fraktale noch einmal als Projektarbeit angeboten.
Im November 1999 wurde von den drei Schülerinnen Maike Mevenkamp, Caroline Schenk und Janina Schlenkert Klasse 10 ein Modell des Ikosaederschwamms Iterationsstufe 2 aus Schreibpapier verwirklicht als Iterationsstufe 2.
2000
Im Frühjahr wurde ein Oktaederschwamm Iterationsstufe 3 aus Schreibpapier
fertiggestellt. Auffallend die Druckfestigkeit.
Versuch eines Dodekaederschwamms in der zweiten Iterationsstufe aus
400 Dodekaedern wurde nicht vollendet.
Ein Bild der ersten Iterationsstufe wird hier gezeigt.
März: Erster Vortrag zu Platonischen Fraktalen in Greifswald bei der Emeritierungsfeier von Prof. Dr. Flachsmeyer
April: Vortrag auf der MNU-Tagung in Stuttgart
Kontakt mit Herrn Dr. Christoph Pöppe, Redaktion Spektrum der Wissenschaft.
Dr. Pöppe hat kopierbare Bausätze für die zweite Iterationsstufe
des Ikosaederschwamms hergestellt (Bezeichnung: 144 Ikosaederknubbel".
Dabei nutzte er aus, daß man die eingeschlossenen inneren unsichtbaren
Flächen auch weglassen kann. Die drei Schülerinnen haben in vielen
Arbeitsstunden aus seiner ersten Bauanleitung ein Modell hergestellt. Im
Nachhinein bezeichnet Dr. Pöppe seine erste Bauanleitung als praktisch
fast undurchführbar, so daß die drei Schülerinnen
eigentlich etwas fast Unmögliches geschafft haben. Inzwischen hat
er den Bausatz, auch im Hinblick auf das Geometrie-Wochenende in München,
zweimal verbessert.
Juli: Ausstellung in Greifswald (Wanderausstellung "Mathematik und Kunst" von Prof. Dr. Schreiber, Uni Greifswald)
Juli/August: Ausstellung in Leipzig (Wanderausstellung "Mathematik und Kunst" von Prof. Dr. Schreiber, Uni Greifswald)
August: Ausstellung " Platonische Fraktale" in der örtlichen Sparkasse
September: Ausstellung in Duisburg (Wanderausstellung "Mathematik und Kunst" von Prof. Dr. Schreiber, Uni Greifswald)
Inzwischen hat Dr. Pöppe auch eine Bauasatz mit Anleitung zum Dodekaederschwamm 1. Stufe produziert.
November:. Veröffentlichung in Spektrum der Wissenschaft
2001
19. Januar: Geometriewochenende in München
Wir sind gespannt!
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen Zurück zur Titelseite
Variationen des Mengerschwamms

Ausstellungsstück Sierpinskitetraeder
Das Kunstwerk mit seinem Künstler
Bastian Wiedeck
im Sommer 1998
(Dritte Iterationsstufe, bestehend aus 64 Tetraedern bzw.
36 Meter Schweißdraht, an den Nahtstellen gelötet, 50
Arbeitsstunden).

Das Ausstellungsstück „Mengerstern“:
Ein Kunstwerk mit seinem Künstler
Peter Graboswki
im Sommer 1998
Die Iteration mit der zum Mengerschwsamm komplementären Operationen.
Die sieben inneren Würfel bleiben und die 20 äusseren
Würfel werden entfernt.
Ein Modell aus 7x7x7 = 343 Styroporwürfeln zum Anfassen(Styroporwürfel),
In QBASIC gezeichnete Varianten zum Mengerschwamm.
1) Alle 27 Würfel bleiben, allerdings in veränderter Größe.
Die acht Eckwürfel werden vergrößert (hier auf verdoppelte
Kantenlänge)
und alle 19 anderen Würfel werden zu kleineren (hier 1/5 der
ursprünglichen Kantenlänge) gestaucht.
a) 26 Würfel in Außenflächenlage bis auf den mittigen
innersten Würfel.

b) alle Würfel werden mittig zurechtgerückt.

Peter Graboswkis Mengerstern aber mir veränderten Größen
der nicht entfernten Würfel.:
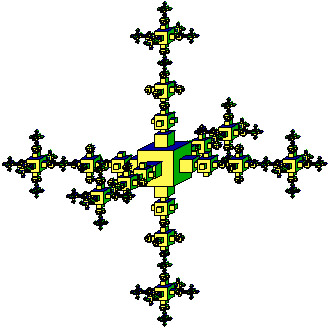
Dritte Iterationsstufe eines fraktalen Weihnachtsbaumes aus dem 7x7x7 Würfel geschnitzt.

Anmerkungen
Bemerkung zu Iterationen in der Schule:
Iteriert werden dort eindimensionale reelle Iterationsfunktionen (z.B. die Linearen Funktionen aber auch das Newtonverfahren ist ein Beispiel), wobei nicht nur die Konvergenz gegen einen Fixpunkt, sondern auch komplexeres (sprich zyklisches und chaotisches) Langzeitverhalten als ein völlig gewöhnliches Verhalten Dynamischer Systeme nahe gebracht werden soll.
Damals 1998 war anscheinend wirklich noch keiner
der in dem Spektrumbeitrag Nov. 2000 und hier publizierten drei fehlenden
platonischen Schwämme veröffentlicht.
Man hat mir gegenüber nach der Spektrumveröffentlichung mehrfach
die Vermutung geäußert, daß es diese Figuren irgendwo
geben müßte, aber noch keinen konkreten Fall explizit genannt.
Im Internet in der Newsgroup "sci.fraktals" habe ich einen russischen
Mathematiker Evgeni Demidov gefunden, der genau unseren Oktaederschwamm
konstruiert hat. Er nennt ihn dort Sierpinski-Oktaeder.
Mit Hilfe von Dr. Pöppe bin ich auf ein zwei Autoren aufmerksam
geworden, die Experimente zu Fraktalen aus platonischen Körpern hergestellt
haben.
Literatur
Sierpinski, Waclaw. Sur une courbe dont
tout point est un point de ramification. Comptes Rendus hebdomadaires
des séances de l'Acadeémie des Sciences 160, p. 302-305 Paris
1915
Menger, Karl "Über die Dimensionalität
von Punktmengen (Erster Teil)" im Jahr 1923 Monatshefte für Mathematik
und Physik (Heft 33), S. 148-160,
und "Über die Dimensionalität von Punktmengen (Zweiter
Teil)", im Jahr 1926, Monatshefte für Mathematik und Physik (Heft
34), S: 137-161(?)
Menger, Karl. "Allgemeine Räume und
Cartesische Räume". Zweite Mitteilung: "Über umfassendste n.dimensionale
Mengen". Proceedings Academie Amsterdam 29, S. 1124ff, 1923
Blumenthal, Leonhard M./ Menger Karl. Studies
in Geometry. W. H. Freeman and Company Sanfrancisco 1970
Mandelbrot, Benoît B. Fraktale Geometrie
der Natur 1987 (engl. Orig. 1977)
Mandelbrot, Benoît B.Les objets fractals:
forme, hasard et dimension In: Flammarion. Paris 1975
Urysohn, M. P. "Les multiplicites cantoriennes"
Comptes Rendus hebdomadaires des séances de l'Acadeémie des
Sciences 175 II p. 440-442 Paris 1922
M. Komorek/ R. Duit/ M. Schnegelberger
(Hrsg.). Fraktale im Unterricht.
IPN-Materialien. Kiel 1998
W. Sternemann. Das "Schneeflockenmeter". Ein
Denkanstoß zum Messen von Schneeflockenkurven. In M. Komorek/
R. Duit/ M. Schnegelberger (Hrsg.), Fraktale im Unterricht IPN-Materialien
Kiel 1998
Hausdorff, Felix Dimension und äußeres
Maß Mathematische Annalen 79 S.157-179, 1919
*) Für die Hilfe bei der Zusammenstellung
danke ich Herrn Prof. Dr. Hans Joachim Samaga
Universität Hamburg - FB Mathematik
Platonische Fraktale Zu zwei klassischen platonischen Fraktalen